・6年生の学習は難しくてもう教えられない
・6年生の算数でつまずきやすいところは?
・教え方がわからない

お家でお子さんの勉強をみていると,こんなことを思うことはよくあります。この記事では,6年生算数についてポイントを紹介します。
自分のお子さんに関係するところを繰り返し確認し,日々のサポートにつなげてください。
6年生の算数は,これまでの学習内容を全て使います。
1~5年生のまでの算数は,全て6年生の学習内容に
つながるということです。
算数が積み上げの教科だと言われる所以ですね。
そして,中学校の学習内容も意識しながら
学習を進めることで,中学校への接続がスムーズになります。

このページでは,6年生算数の中でつまずきやすい内容について触れていきます。
☆他の学年の算数について☆
・1年生の算数 ・2年生の算数 ・3年生の算数 ・4年生の算数 ・5年生の算数
☆この記事でわかること☆
✔つまずきやすい学習内容 ✔つまずきやすい理由 ✔どのようにサポートしてあげればいいか
分数のかけ算・わり算は問題から式を立てるのが難しい


分母は分母同士かける,分子は分子同士かける・・・ということはあっという間に理解します。約分さえ間違わなければ,答えも容易くだせます。つまずくのは立式です。
たとえばこんな問題があったとします。
ここに2/7mの長さの棒がありました。この棒の重さは2/5㎏です。この棒1mの重さは何㎏でしょうか。
かなりの確率で2/7÷2/5と間違えます。
どっちでどっちをわったらいいかわからないから,
とりあえず数字が出てきた順に使ってみよう。
というよくある発想です。
学校では,よく数直線を使って考えさせます。
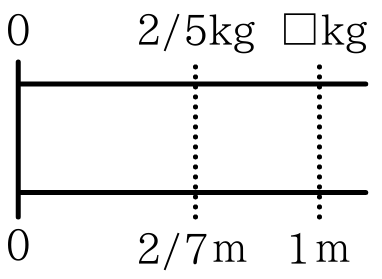
関係性がわかりますからね。この数直線から考えると,
1mを2/7mの関係性は,1m×2/7=2/7mとなっています。 だから重さの方も同様で,□m×2/7=2/5mということになります。 □×2/7=2/5だから □=2/5÷2/7となります。

どうやらこの理屈が子どもにとってはややこしい場合があるようです。

だから私なら上記のような考え方は一通り教えた後,次のように教えます。
今回は1mあたりの重さを知りたいんです。 だから,㎏÷mをすれば,1mあたりの重さがわかります。 なぜなら,「わり算は1つ分(1あたり量)を求める計算方法」だからです。 つまり,今回の問題とは逆に,1kgあたりの長さを聞かれたら, m÷㎏にすれば答えが出ます。 この考え方の根本はわり算という計算方法の意味です。
これを覚えておけば,どんな問題が出ても対応できます。
1mあたりなのか,1㎏あたりなのか,
1時間あたりなのか,1Lあたりなのか,
そこさえ整理できれば,迷いません。
わざわざ数直線をかく必要もありません。

難しいことをややこしく教えるのではなく,単純化してあげることが重要ですね。
円の面積は計算ミス多し!

公式【半径×半径×円周率】を覚えるのは簡単です。
なぜ,その公式で求めることができるのかを説明するのが難しいです。
また,この学習では計算ミスが多いです。
円の公式の証明は,この学習のはじめに行います。
一般的には,円を複数の扇形に切り分けつなげていくと,
既習内容である長方形になるということから考えます。
→詳しく知りたい方はこちら←(おかわりドリルより)
そして,この学習で一番の課題は,
計算ミスが本当に多いことです。
なぜなら円周率=3.14なので,
小数のかけ算がどうしても入ってしまうからです。
また,扇形の面積の求め方も学習します。
教科書には出てきませんが,
「扇形の面積=半径×半径×円周率×中心角/360」
で覚えておくと困らないです。

計算ミスは反復練習しかないですが,高学年でもノートのマスを有効に使うことで,ミスを減らすことができます。
◆スマイルゼミ◆タブレットで学ぶ 【小学生向け通信教育】が誕生!
比例・反比例はxとyの式で表すのに悩む


上の写真は,コインが積み重なっています。
これは,何が何に比例するのかが難しいところなんです。
一方の変化に伴ってもう一方が変化する関係として,
比例と反比例を学習します。
まず,表を見ながら変化の様子をとらえます。
比例でいえば,一方が2倍,3倍となったら
もう一方も2倍,3倍となる・・・
これはわかりやすいんです。
これを式に表すときに苦手さを感じる子が多いです。
例えば次のような問題・・・
| コインの枚数(x) | 1 | 2 | 3 | 4 |
| コイン全体の重さ(y) | 2 | 4 | 6 | 8 |
これは,比例関係なので,式に表すためには,
きまった数(比例定数)を探します。
y÷x=2になるので,決まった数は2です。

ここまでは,だいたいみんなできるんですよね~
このあと,y=きまった数×Xの形に表すときになぜかできなくなります。
なぜか!!!
原因は簡単です。文字式になれていないんです。6年生の算数はほとんどの教科書で,「文字と式」の学習から始まります。一昔前は,xやyなどの文字を含む式は中学校からの学習内容でした。小学校までは,文字ではなく,□を使った式だったんです。しかし,指導要領の改訂により,小学校から学習することになりました。しかし,6年生になってはじめて出てくるので,慣れるのに時間を要する子が出てきます。比例・反比例の場面を文字の式で表せない子は,きっと文字を使って問題場面を表すことになれていません。

だから,ここでつまずいたら,少し前の学習内容である,「文字と式」について復習を重ねてあげることをおすすめします。
もう一つだけ・・・
反比例のグラフは曲線だということは,中学校からです。
しかし,小学校でも扱っていいと思います。
なぜ,x軸,y軸と交わらないのか,
式に0を代入させて考えると,
0でわることはできないということを再確認できます。
比~全体から一部を求めるのが困難


比は生活の中でも使う場面が多いです。
比の学習でつまずくポイントは1点のみ
全体から1部を求めるときです。

なんのこっちゃ・・・って感じですよね。
たとえば,次のような問題のときです。
ここにコーヒー牛乳が600mlあります。このコーヒー牛乳はコーヒーと牛乳が3:5になるように混ぜてあります。さて,コーヒーと牛乳はそれぞれ何mlでしょうか。
比の問題を解くときに,比の式に表して考えますが,
ここでよくある間違いが,
3:5=X:600とか,3:5=600:Xです。
3:5がそのまま使えるのは,
一方の量が分かっているときだけです。
しかし,上記の問題はどちらもわかってないんです。

じゃあどうすればいいか,言葉で整理してあげましょう。
コーヒー:牛乳=わからないml:わからないml
これでは解けないということに気づかせることが1歩目です。
ここでわかっている量は600mlだけなので,
コーヒーの量をXと置くと,
X:600=コーヒー:全体
コーヒー:全体=3:(3+5)

ここで大切なことは,全体を表す比は,双方の比を足した数,ここでは3:5なので3+5=8ということになります。
ここまでくれば,
コーヒー:全体=3:(3+5)
コーヒー:全体=X:600
この2つの式から
3:8=X:600
という式がたてられます。

算数が苦手な子ほど,問題の状況を整理することが苦手です。
はじめのうちは,大人が図や言葉を書きながら説明してあげることが大切です。
いったん理解したら,あとはどんな問題にもチャレンジするようになります。
まとめ~他の学習内容についても紹介
高学年になると,学習内容も難しく,
子どもに聞かれたときにパッと答えられないものもあります。
もし,この記事で紹介した内容でつまずいていましたら,
是非この記事を参考にサポートしてあげてください。

最後に他の学習内容について紹介します。
・文字を使った式(XとYを使います)
・対称な図形(線対称・点対称)
・データの見方(平均値・中央値など)
・角柱と円柱の体積(底面積×高さで全部できる)
・拡大図と縮図(合同条件使います)
・並び方と組み合わせ(樹形図使います)

最後まで読んでくれてありがとうございました。










コメント